Total Emission

Blackbody

Definition:

• At a given temperature and wavelength, no body can emit more than a blackbody
• Absorbs all incident radiation
• Emits in all directions

$E_b$ is emissive power = radiated power per unit surface area ($W/m^2$)
$\sigma$ is the Stefan-Boltzmann constant $\sigma =5.67\ast {10}^{-8}W/m^2{K}^4$
$T$ is the surface temperature ($K$)

Examples:

Example 1 - Sun

Example 2 - Human Body

Spectral Emission

Spectral Emissive Power:

• aka spectral radiant emittance
• Power per unit surface area per wavelength
• Units: $W/m^{2}m$

Planck's Distribution:

Wien's Displacement Law:

• Wavelength of peak radiation:

Examples:

Example 1 - Sun

• Surface temperature: $T=5800K$
• Peak radiation at: ${\lambda }_{max}=500nm$ (visible range)

Example 2 - Human Body

• Skin temperature: $T\approx 33C=306K$
• Peak radiation at: ${\lambda }_{max}\approx 9.5\mu m$ (infrared)

Example 3 - Earth

• Average air temp: $T\approx 15C$
• Range: $T\approx \pm 50C$ (Infrareds)

Example 4 - Flame

• Burnt temperature: $T_b\approx 2000K$
• Peak radiation at: ${\lambda }_{max}\approx 1.4\mu m$ (infrared)

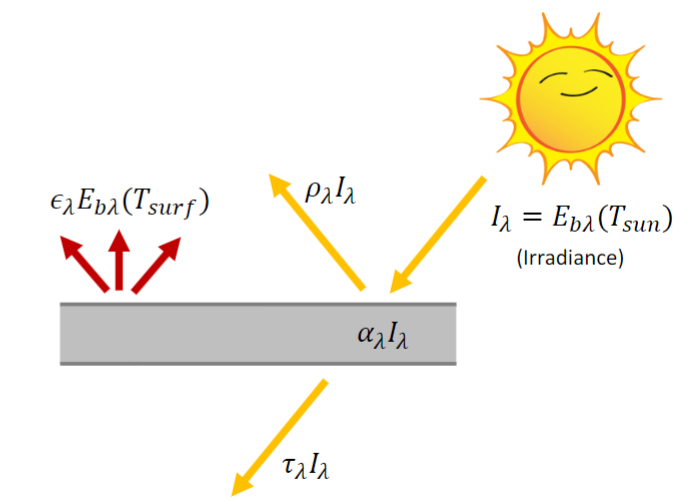
Non-Blackbody

Definitions:

• Absorptivity (${\alpha }_{\lambda }$) - Fraction of incident radiant energy absorbed by a surface
• Reflectivity (${\rho }_{\lambda }$) - Fraction of incident radiant energy reflected by a surface
• Transmittivity (${\tau }_{\lambda }$) - Fraction of incident radiant energy passing through surface
• Emissivity (${ϵ}_{\lambda }$) - Fraction of blackbody radiation emitted by the surface

Key properties:

• Reflected and transmitted at same wavelength
• Emitted at different wavelength

Special case: Blackbody

• ${\alpha }_{\lambda }={ϵ}_{\lambda }=1$
• ${\rho }_{\lambda }={\tau }_{\lambda }=0$
  

Kirchhoff's Law:

Examples:

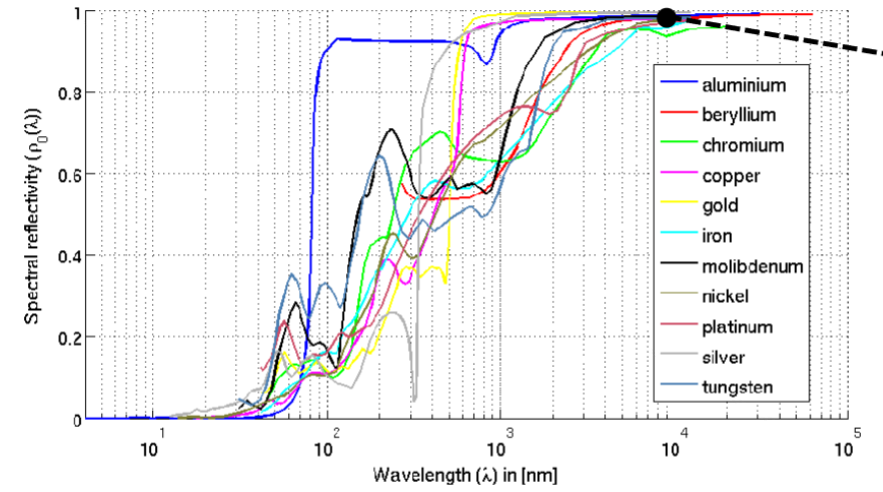
Example 1: Metals

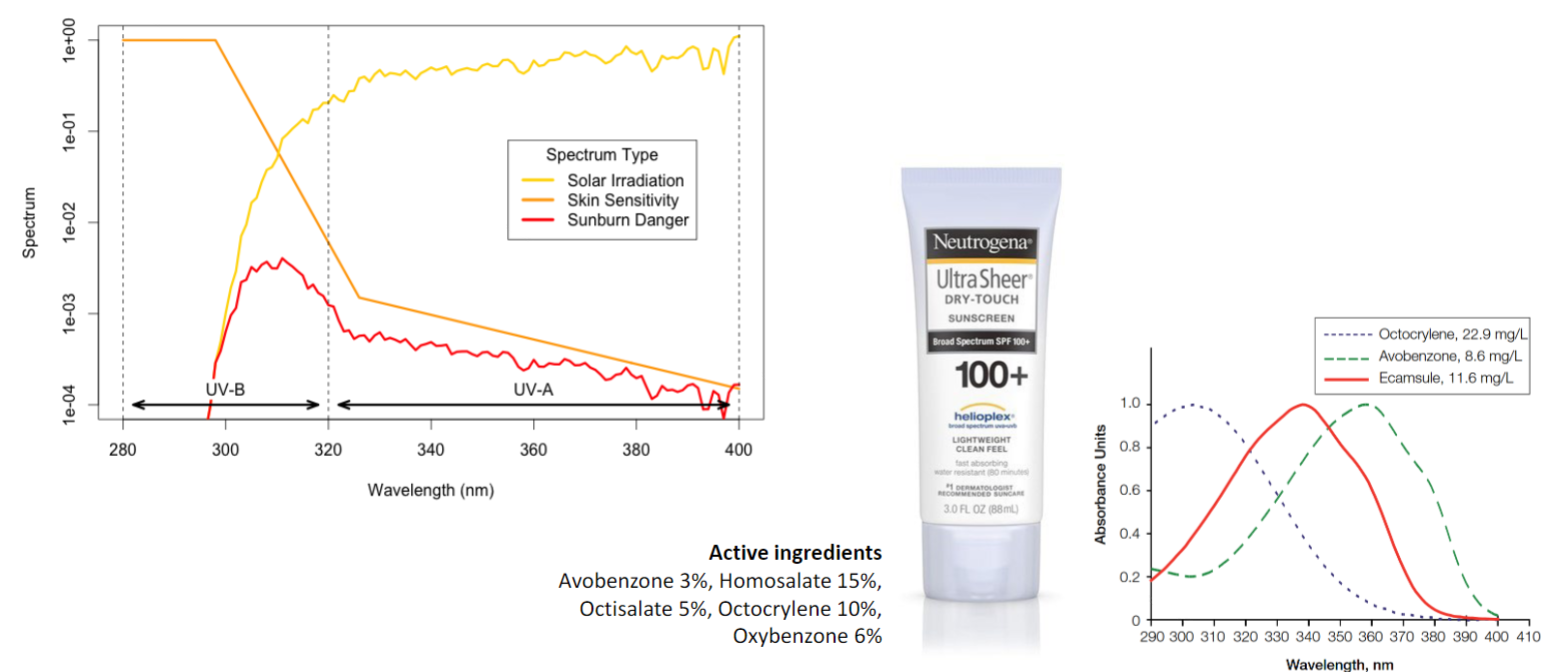
Example 2: Sunscreen

Example 3: Human Skin

Values:

• Skin temperature: $T\approx 33\mathrm{°}C=306K$
• Peak radiation: ${\lambda }_{max}\approx 9.5\mu m$ (infrared)

Special case: Gray body

• Not color gray
• Constant Emissivity: ${ϵ}_{\lambda }=ϵ$