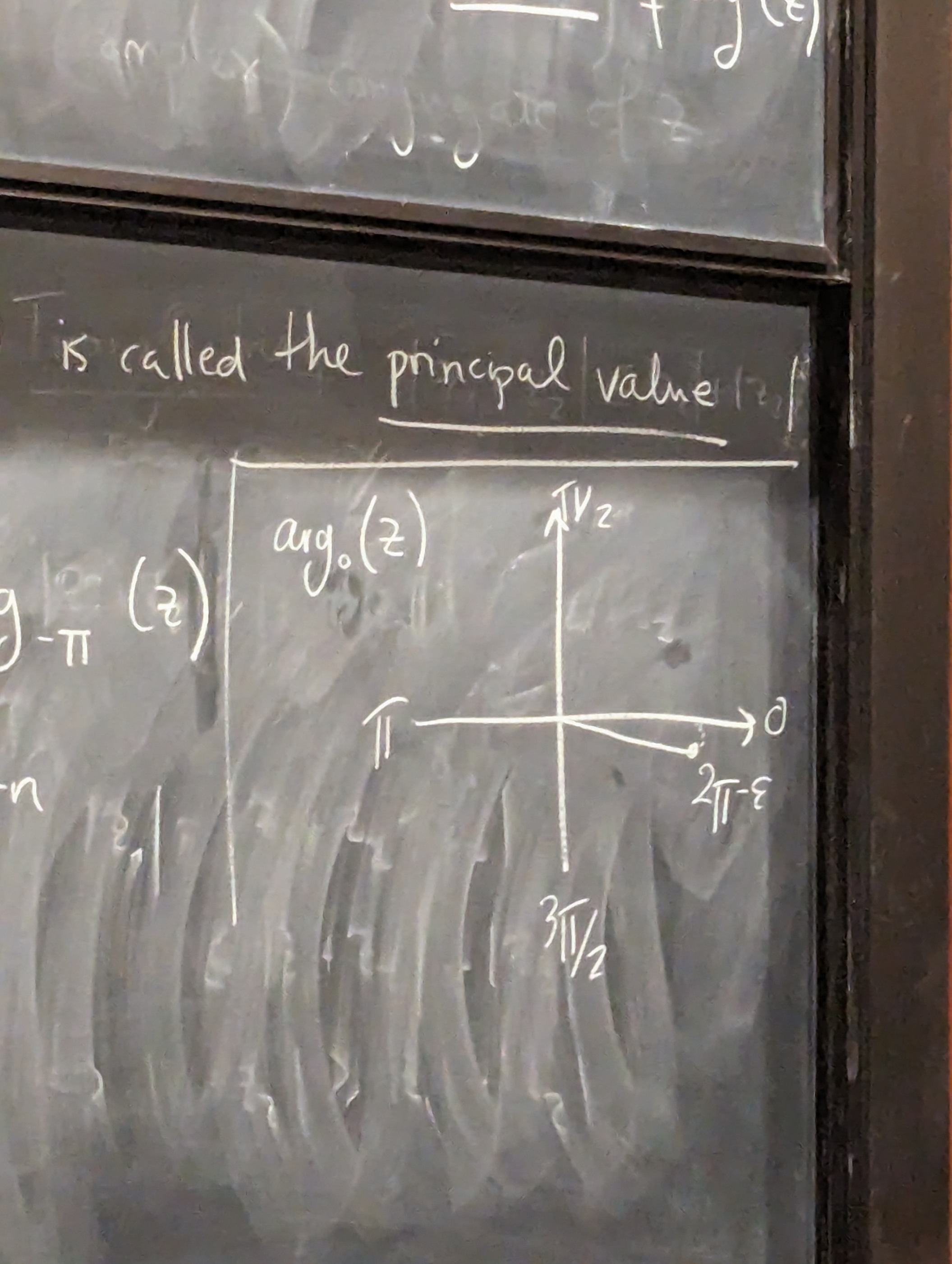Polar Form

$(r, θ)$ are the polar coordinates of $(x, y)$ .

Polar form of $z$

${\begin{cases} x = r \cos θ \\ y = r \sin θ \end{cases} \Rightarrow z = r (\cos θ + i \sin θ)$

Remark:
If $z = 0$ , then $θ$ undefined. (Assume $z \neq 0$ if in polar form).

$r = \sqrt{x^{2} + y^{2}} = | z |$ where $r$ is uniquely defined.
$(r, θ), (r, θ + 2 π), \dots, (r, θ + 2 n π) \to$ give same $(x, y)$

Argument of $z$

Definition

The set of all angles is called the argument of $z$ . $a r g (z) = θ + 2 π n$ $n \in Z$ .

Remark:
$f (z) = a r g (z)$ multivalued function.

Example 1:

$a r g (i) = \frac{π}{2} + 2 π n$ , $n = 0, \pm 1, \pm 2, \dots$
Any half-interval $[θ_{0}, θ_{0} + 2 π)$ will contain one value of $a r g (v)$ .

Branch of $a r g (z)$ :

Definition

$a r g_{θ_{0}} (z) = a r g (z) \cap [θ_{0}, θ_{0} + 2 π)$ is called a branch of $a r g (z)$ .
The branch $a r g (z)$ is called the principal value of the argument of $z$ .
$A r g (z) = a r g_{- π} (z)$

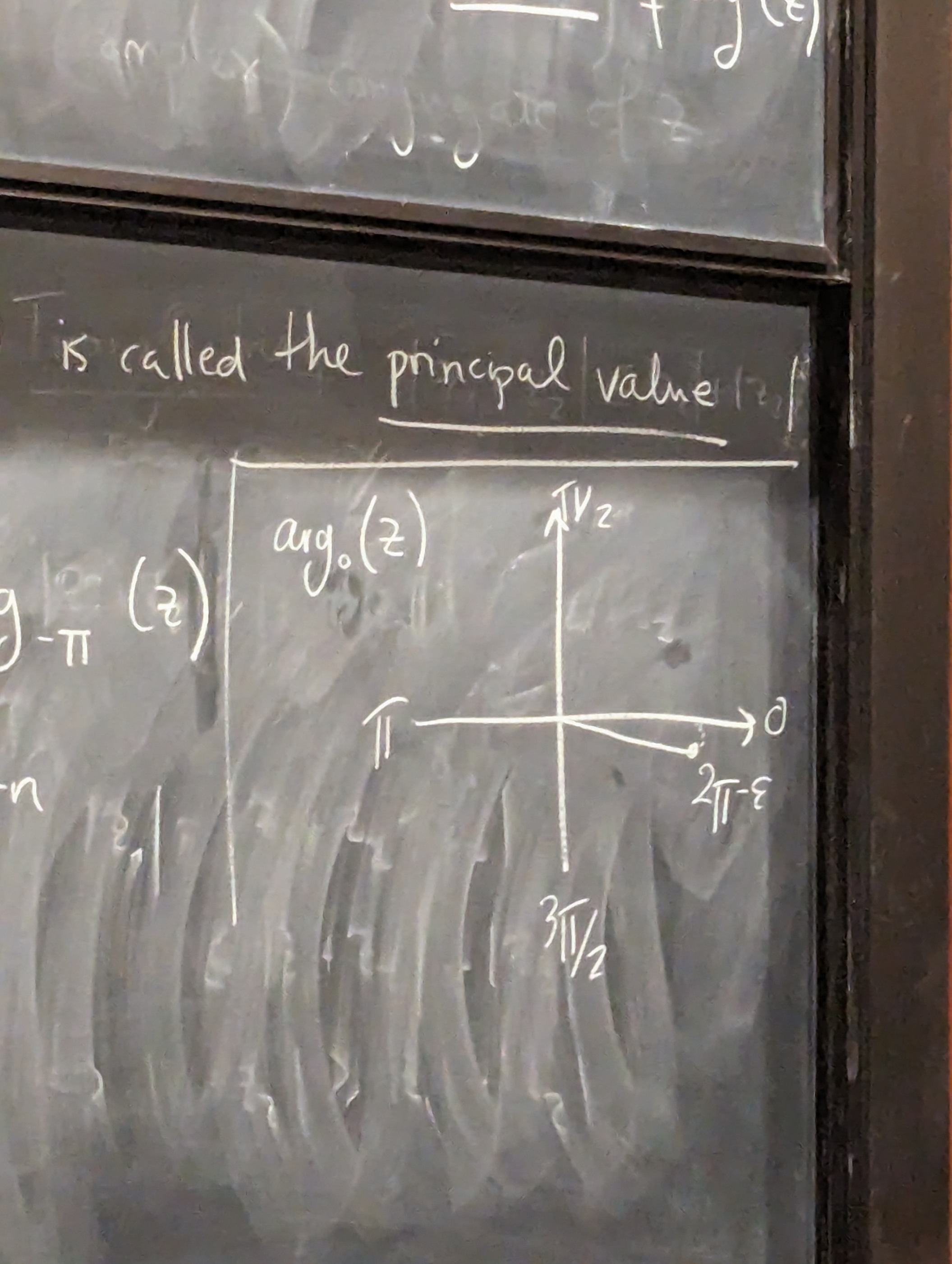
PXL_20240103_195307069 1.jpg

Remark:
$a r g (z) = a r g_{θ_{0}} (z) + 2 π n$

$A r g (- 1) = - π$
$[- π, π)$
$a r g_{0} (- 1) = π$
$[0, 2 π)$
$A r g (x + i y) = s i g n (y) \cdot \arccos (\frac{x}{\sqrt{x^{2} + y^{2}}})$ for $z \notin$ branch cut. Note $s i g n \neq s i n$

Polar form of z

Argument of z

Branch of arg(z):

Polar form of $z$

Argument of $z$

Branch of $a r g (z)$ :