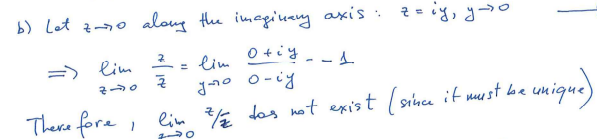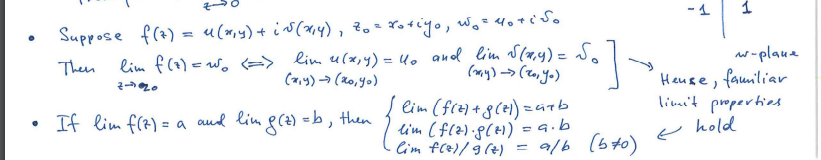Functions of Complex Numbers

In the real calculus, the main theorems are usually stated for functions defined on an open or closed interval. In complex analysis, the main results are formulated for functions defined on 2-dimensional subsets of $C$ , called "domains" or "closed regions" (which are in some sense generalizations of open/closed intervals).

In the study of complex functions, our objective is to mimic the concepts, theorems, and mathematical structure of real calculus. In particular, we want to understand how to differentiate and integrate functions of a complex variable. It will turn out that, while the concepts of limits and continuity are similar to that of real variables, the notion of a derivative is far more subtle and interesting in the complex case because of the intrinsically two-dimensional nature of the complex variable.

Definition

A function $f$ defined on $S \subset C$ is a rule that assigns to each $z \in S$ a complex number $w \in C$ , $w = f (z)$ .
The set $S$ is called the domain of definition. It is often a domain but it does not need to be so.
The set $R = {w : w = f (z), z \in S}$ is called the range.

Examples:

If $n \in N$ and $a_{0}, a_{1}, \dots, a_{n} \in C \Rightarrow p (z) = a_{0} + a_{1} z + a_{2} z^{2} + \dots + a_{n} z^{n}$ is a polynomial of degree $n$ if $a_{n} = 0$ .
If $p (z)$ and $q (z)$ are polynomials $\Rightarrow r (z) = \frac{p (z)}{q (z)}$ is a rational function whose domain of definition is ${z : q (z) \neq 0}$

Remark: Leter on we will define other elementary functions: $e^{z}$ , $\log z$ , $z^{α}$ where $α \in C$ , trigonometric function. We will do this later since some of these functions will turn out to be multivalued (like $\arg (z)$ ), and so some care is required in handling them. Our current focus is on single-valued functions.

Let's rewrite the expression $w = f (z)$ in terms of real and imaginary parts. Let $z = x + i y$ and $w = u + i v$ . Then $w = u + i v = f (x + i y) - ℜ (f (x + i y)) + i ℑ (f (x + i y))$ . Thus $w = f (z) = u (x, y) + i v (x, y)$ . So in essence, a complex valued function of a complex variable is a pair of real functions of two real variables: $u (x, y)$ and $v (x, y)$ .

Example:

Let $w = f (z) = z^{2}$ . Then $w = (x + i y)^{2} = x^{2} - y^{2} + i 2 x y$ ${\begin{cases} u = x^{2} - y^{2} \\ v = 2 x y \end{cases}$ .
Geometrically, it is useful to think about a function $w = f (z)$ as a mapping or transformation of the points $(x, y)$ in the $z$ -plane to the points $(u, v)$ in the $w$ -plane. We can't plot a graph of a complex function $w = f (z)$ since this would require four dimensions $(x, y, u, v)$ , but we can visualize complex functions by sketching how regions in the $z$ -plane transform to the corresponding regions in the $w$ -plane.

Example:

$w = f (t) = \bar{z}$ maps $ℑ (z) > 0$ into $ℑ (w) < 0$ and $ℑ (z) < 0$ into $ℑ (w) > 0$ . ${\begin{cases} u = x \\ v = - y \end{cases}$

Limits of Complex Functions:

Suppose $w = f (z)$ is defined in a deleted (excluding $z_{0}$ ) neighborhood of $z_{0}$ .

Definition

We say that $f (z)$ has the limit $w_{0}$ as $z$ approaches $z_{0}$ and write $lim_{z \to z_{0}} f (z) = w_{0}$ if $\forall ϵ > 0 \exists δ > 0$ such that $| f (z) - w_{0} | < ϵ$ whenever $0 < | z - z_{0} | < δ$ . Intuitively, $lim_{z \to z_{0}} f (z) = w_{0}$ means that we can make $f (z)$ arbitrarily close to $w_{0}$ by taking $z$ sufficiently close to $z_{0}$ . Geometrically, for any $U_{ϵ} (w_{0})$ there exists a deleted neighborhood ${\dot{U}}_{δ} (z_{0})$ such that $f ({\dot{U}}_{δ} (z_{0})) \subset U_{ϵ} (w_{0})$ .

Properties:

If $lim_{z \to z_{0}} f (z)$ exists, it is unique.
$lim_{z \to z_{0}} f (z) = w_{0} \Rightarrow$ for any sequence ${z_{n}}$ converging to $z_{0}$ , the sequence ${f (z_{n})} \to w_{0}$ as $n \to \infty$ .
Thus, if $lim_{z \to z_{0}} f (z)$ exists, it does not depend on the way $z$ approaches $z_{0}$ , $z$ can approach $z_{0}$ from any direction in the complex plane and we will get the same $w_{0}$ .

Example:

Let's try to find $lim_{z \to 0} \frac{z}{\bar{z}}$ :

Let $z \to 0$ along the positive real axis: $z = x, x \to 0 \Rightarrow lim_{z \to 0} \frac{z}{\bar{z}} = lim_{x \to 0} \frac{x + i 0}{x - i 0} = 1$